일반적인 1차, 2차 지연 제어계에서의 과도응답을 살펴보도록 하겠습니다. 두 가지 경우 모두 입력은 단위계단입력 r(t)=u(t)일 때를 고려하겠습니다.
1. 1차 지연 제어계의 과도 응답
일반적인 1차 지연 제어계의 전달함수는 다음과 같습니다.

입력 r(t)=u(t)를 고려하므로, R(s)=1/s를 위 식에 대입해 응답 C(s)로 정리하면,
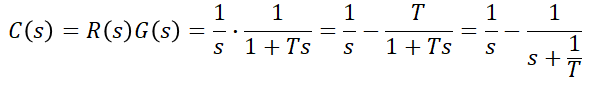
역 라플라스 변환을 위해 부분분수 전개를 하였고, 과정은 생략하였습니다. 결국 응답은 다음과 같습니다.

이를 그래프로 표현하게 되면,

위와 같이 나타나게 됩니다.
1차 지연제어계에서 단위계단입력일때, 응답특성은 전달함수의 T값에 따라 변한다는 것을 알 수 있습니다.
2. 2차 지연 제어계의 과도 응답
이 2차 지연 제어계의 과도 응답은 잘 기억하셔야 합니다. 먼저 일반적인 2차 지연 제어계의 전달함수를 보면

이며, 역시 입력을 단위계단입력인 r(t)=u(t)를 대입하게 되면 출력 C(s)는

여기서 분모항의 2차식을 인수분해하면,

역 라플라스 변환을 위해 부분분수전개를 하면,
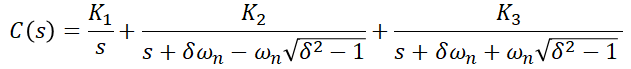
이를 역 라플라스 변환을 하게 되면 구하고자 하는 2차 지연제어계의 응답을 구할 수 있습니다.
그런데, 그 전에 먼저 이 식을 통해 알 수 있는 것은 wn은 고유진동각주파수로 변화하지 않는 값이기 때문에 δ값에 의해 특성근의 위치를 결정한다는 것을 알 수 있습니다. 따라서 각각의 δ값의 범위에 따라 그 의미를 살펴보면 다음과 같습니다.
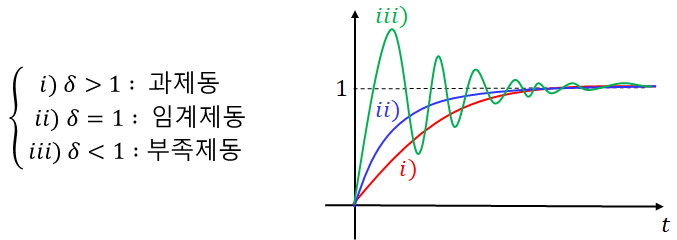
위와 같이 δ값에 따라 제어계의 출력특성이 달라지고, 위와 같은 그래프로 나타난다는 것을 알 수 있습니다. 이 δ값에 대해 조금 더 자세히 살펴보도록 하겠습니다.
3. 특성방정식의 근의 위치별 과도 응답
위에서 살펴본 일반적인 2차 지연 제어계의 전달함수는 아래와 같은 형태였습니다.

그럼 이 식에서 특성방정식을 찾아보면 다음과 같습니다.

이 2차방정식의 근이 바로 특성근이므로 그 근을 구하면,

근의 공식을 이용하면 간단하게 계산할 수 있습니다.
이제 이 근들을 δ값에 따라 복소평면상의 위치가 달라지므로 δ값의 범위에 따라 근위 위치가 어디에 자리하는지 살펴보도록 하겠습니다.
1) δ>1 (과제동) : δ가 1보다 크므로 특성근은 다음과 같습니다.

즉, 근호 안의 값이 1보다 크기 때문에 음의 서로다른 실근임을 알 수 있습니다.
2) δ=1 (임계제동) : 근호 안의 값이 0이 되므로 특성근은 다음과 같습니다.

임계제동은 특성근이 중근을 가질 때라는 것을 알 수 있습니다.
3) 0<δ<1 (부족제동) : δ값이 1보다 작으므로 근호 안이 음수가 되어 특성근은 다음과 같습니다.

이 때는 특성근이 음의 실수부를 갖는 공액복소근이 됩니다.
4) δ=0 (무제동) : δ=0을 대입하면 근은 다음과 같습니다.

허수축 상에 두 근이 존재하게 된다는 것을 알 수 있습니다.
이 근들을 복소평면에 표현해보면,
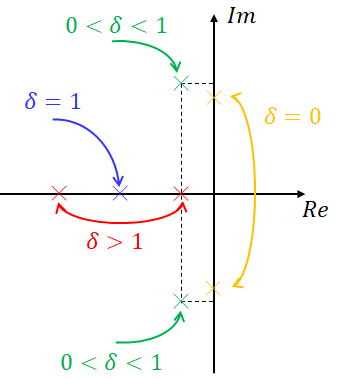
이렇게 위치하고 있습니다. 즉, 출력을 일정한 값으로 수렴하게 하는 근은 복소평면상 좌반면에 존재해야 합니다. 이후에도 계속해서 나오지만 이렇게 특성근의 위치를 통해 제어계가 안정한지를 알 수 있습니다.
'전기 > 제어공학' 카테고리의 다른 글
| [제어공학] 7. 과도응답의 시간특성 및 정상편차 (0) | 2020.01.22 |
|---|---|
| [제어공학] 6. 특성방정식의 근의 위치별 응답특성 (1) | 2020.01.22 |
| [제어공학] 4. 특성방정식 (6) | 2020.01.20 |
| [제어공학] 3. 자동제어계의 과도응답 (0) | 2020.01.20 |
| [제어공학] 2. 신호흐름선도 (1) | 2020.01.17 |



