자동제어계의 과도응답에서 말하는 응답이란 간단하게 지금까지 살펴보았던 출력시간함수 c(t)를 의미합니다. 이 응답을 알아보기 위해 먼저 간단한 제어계를 살펴보겠습니다.

여기서 지난번에 살펴본 것 처럼 G(s)=C(s)/R(s)이므로, C(s)=R(s)G(s)라는 것을 알 수 있었습니다.

이 식을 역 라플라스변환하게 되면,

로 표현할 수 있습니다. 즉, 과도응답 c(t)를 구하기 위해선 입력 R(s)가 어떤 입력인지 알아야합니다. 따라서 기본적인 다음의 네 가지의 입력을 알아보고 각각의 입력에 대한 응답을 살펴보도록 하겠습니다.
1. 입력의 종류
1) 계단 입력

여기서 u(t)를 연속시간 단위 계단 신호라고합니다.

(2) 임펄스 입력

(3) 경사 입력 : 등속 입력이라고도 합니다.
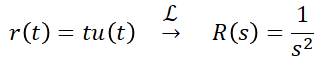
(4) 포물선 입력 : 등가속 입력이라고도 합니다.
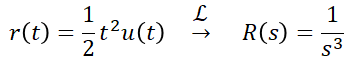
각각의 입력이 갖는 의미에 대해서는 이후에 다뤄보도록 하고, 이 입력들에 대한 각각의 응답을 보겠습니다.
2. 입력에 따른 응답
1) 단위 계단 응답(인디셜 응답)
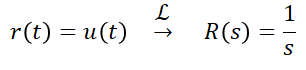
단위 계단 응답이므로 위에서 살펴보았던 상수 k=1인 경우를 의미합니다. 그럼 이 때의 응답을 보면,

이므로, G(s)가 주어졌다면 간단하게 응답을 구할 수 있습니다. 예제를 통해 조금 더 살펴보도록 하겠습니다.
ex.1) G(s)=1/(s+1)일 때, 단위 계단 응답 c(t)=?
위에서 살펴 본 것처럼 단위 계단 응답을 구해야 하므로 입력 r(t)=u(t), R(s)=1/s라는 것을 알 고 있습니다. 이를 위 식에 대입해보면,
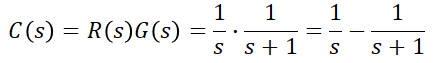
이므로 이를 역 라플라스 변환하게 되면,

로 간단하게 단위 계단 응답을 구할 수 있습니다.
ex.2) 단위 계단 응답 c(t)=1-e^(-2t)일 때, G(s)=?
이번에는 단위 계단 응답을 알고 있을 때 전달함수를 구해보도록 하겠습니다. 역시 단위 계단 응답이므로 r(t)=u(t), R(s)=1/s이고, G(s)를 구하기 위해 응답을 라플라스변환하면,

이므로, 우리가 알고 있는 G(s)=C(s)/R(s)에 대입하여
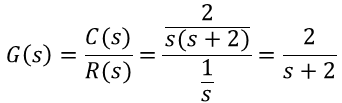
가 된다는 것을 알 수 있습니다.
2) 임펄스 응답
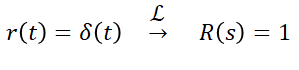
입력이 위와 같으므로
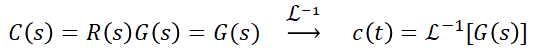
와 같이 구할 수 있습니다.
ex.3) G(s)=1/(s+a)^2 일 때, 임펄스 응답 c(t)=?
이렇게 문제에서 임펄스 응답을 구하라 하지만, 상수에 대한 언급이 없다면 단위 임펄스 응답을 구하시면 됩니다. 즉, R(s)=1을 위 식에 대입해 정리하면,

위와 같이 응답을 구할 수 있습니다.
ex.4) 임펄스 응답 c(t)=e^(-2t)일 때, G(s)=?
임펄스 응답에서 입력 R(s)=1이므로, G(s)=C(s)가 되어 간단하게 구할 수 있습니다.
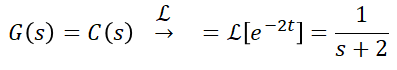
3) 경사응답(등속응답, 램프응답)

이므로, 역시 C(s)=R(s)G(s)식에 대입하게 되면,

를 통해 응답을 구할 수 있습니다.
ex.5) G(s)=(s+1)/(s+2) 일 때, 경사 응답 c(t)=?
역시 특별한 언급이 없으므로 단위 경사 입력임을 가정하고, R(s)=1/s^2를 대입하면,

라플라스 변환을 위한 부분분수화를 위해 위와 같이 나누고 각각을 구하면,

따라서 C(s)를 다시 쓰면,
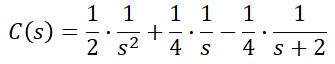
이를 역 라플라스변환하면
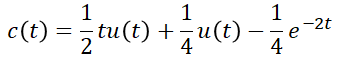
로 경사응답을 구할 수 있습니다.
4) 포물선 응답(등가속 응답)
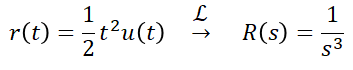
여기서 입력 r(t)의 1/2는 라플라스 변환 시 편의를 위해 임의로 추가한 값입니다. 같은 방법으로 C(s)는
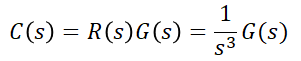
이므로, 이를 통해 응답을 구할 수 있습니다.
'전기 > 제어공학' 카테고리의 다른 글
| [제어공학] 6. 특성방정식의 근의 위치별 응답특성 (1) | 2020.01.22 |
|---|---|
| [제어공학] 5. 1차, 2차 지연 제어계의 과도 응답 (1) | 2020.01.20 |
| [제어공학] 4. 특성방정식 (6) | 2020.01.20 |
| [제어공학] 2. 신호흐름선도 (1) | 2020.01.17 |
| [제어공학] 1. 블록선도 (10) | 2020.01.16 |



