1. 과도응답의 시간 특성
과도응답의 시간 특성을 살펴보기 위해 부족제동인 2차 지연 제어계의 인디셜 응답을 보도록 하겠습니다.

이런 응답으로부터 우리가 알 수 있는 시간특성은 4가지가 있습니다.
1) 오버슈트 : 응답 중에 발생하는 입력과 출력 사이의 최대 편차량을 말합니다. 그러나 이 오버슈트는 백분율 오버슈트를 이용하는 경우가 많고 의미는 다음과 같습니다.

2) 지연시간 (Td) : 정상값의 50%에 도달하는데 걸리는 시간
3) 상승시간 (Tr) : 정상값의 10%~90%에 도달하는 시간
4) 정정시간 (Ts) : 허용 오차 범위 안에 들어오는 시간 (±2~5%)
모두 정상값(최종값)을 기준으로 하고 있으므로, 전달함수나 응답을 통해 최종값을 구할 수 있다면 각각의 값들을 구하는 것은 크게 어렵진 않습니다.
ex.1) 단위 계단 입력에 대한 출력 응답 특성이 c(t)=1-e^(-2t)일 때, 지연시간을 구하시오.
지연시간은 정상값의 50%에 도달하는데 걸리는 시간이므로 먼저 정상값을 구해야 합니다. 그런데 문제에서 출력 응답 특성 c(t)가 주어졌으므로, 간단하게 시간 t를 무한대로 보내 정상값을 구할 수 있습니다.

정상값이 1이므로, 지연시간은 최종값의 50%에 도달하는 시간이므로 응답 c(t)가 0.5가 되는 시간 t를 구하면 되겠죠?

따라서 Td를 계산하면,

으로부터

이므로 밑이 e인 로그를 양변에 취해주도록 하겠습니다.


로 구할 수 있습니다. 같은 방법으로 상승시간과 정정시간 모두 구할 수 있습니다.
2. 정상편차
1) 편차 : 응답과 입력의 차이를 편차라합니다.
이 편차를 살펴보기 위해 앞서 알아본 단위 Feed-back 제어계를 다시 보겠습니다.

바로 이 E(s)가 편차함수입니다. 일반적인 Feed-back제어계도 위와 같이 단위 Feed-back제어계로 만들 수 있으므로 이 경우에서 설명드리도록 하겠습니다.
위 블록선도에서 바로 알 수 있듯이 편차함수 E(s)는 다음과 같습니다.

전체 전달함수를 M(s)라 하면,
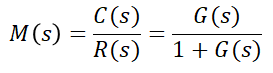
또, 출력에 대한 식을 다시 쓰면,

그럼 이 식들을 위 편차함수 식에 대입해 정리하면,





로 구할 수 있습니다.
2) 정상편차
정상편차는 제어계가 정상상태에 도달했을 때 편차이므로 시간 t를 무한대로 보냈을 때의 편차입니다.

그러나 위에서 라플라스변환을 통한 s함수로 표현하고 있어 최종값 정리에 의해 다음과 같이 쓸 수 있습니다.


이 식으로 부터 알 수 있듯이 분자항의 R(s)로 인해 입력에 따라 편차의 종류가 변한다는 것을 알 수 있습니다. 또한, 분모항의 1+G(s)가 0이 아닌 값을 가져야 편차가 나타날 수 있으므로 편차의 존재를 결정짓는 것은 G(s)가 됩니다.
그럼 다음에 이어서 이 G(s)의 형과 입력 R(s)에 의해 편차가 어떻게 변화하는지 알아보겠습니다.
'전기 > 제어공학' 카테고리의 다른 글
| [제어공학] 9. 주파수 응답과 벡터 궤적 (2) | 2020.01.22 |
|---|---|
| [제어공학] 8. 형에 의한 제어계의 분류 및 입력에 따른 정상편차 (0) | 2020.01.22 |
| [제어공학] 6. 특성방정식의 근의 위치별 응답특성 (0) | 2020.01.22 |
| [제어공학] 5. 1차, 2차 지연 제어계의 과도 응답 (1) | 2020.01.20 |
| [제어공학] 4. 특성방정식 (6) | 2020.01.20 |



