이어서 중거리 송전선로에 대해서 살펴보도록 하겠습니다.
2. 중거리 송전선로
1) 4단자 정수
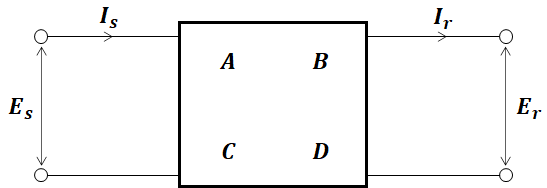
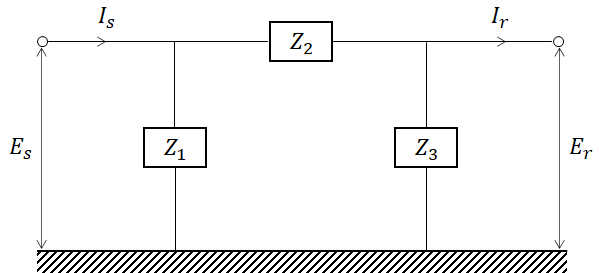
4단자망은 아래의 그림과 같이 임의의 선형 회로망에 대해 입력측과 출력측에 각각의 변수의 상호관계(파라미터)로 표시됩니다.
그리고 아래와 같이도 표현할 수 있습니다.
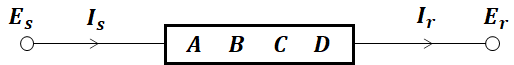
여기서,

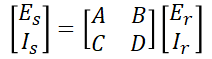
로 나타낼 수 있습니다. 여기서 A, B, C, D 파라미터의 의미는 다음과 같습니다.
(1) A : 개방 역방향 전압 이득 (전압비)
수전단 전류가 0일 때 송전단 전압과 수전단 전압의 비를 의미합니다.
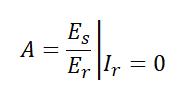
(2) B : 단락 역방향 전달 임피던스
수전단 전압이 0일 때(단락) 역방향 전달 임피던스를 의미합니다.

(3) C : 개방 역방향 전달 어드미턴스
수전단 전류가 0일 때(개방) 역방향 전달 어드미턴스를 의미합니다.
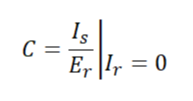
(4) D : 단락 역방향 전류 이득 (전류비)
수전단 전압이 0일 때 송전단 전류와 수전단 전류의 비를 의미합니다.
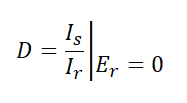
이런 의미를 가진 A, B, C, D의 파라미터 사이에는 다음과 같은 관계가 항상 성립합니다.
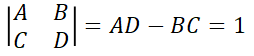
또한, 대칭 4단망의 경우에는 A=D의 관계가 성립합니다.
2) 중거리 송전선로의 해석
중거리 송전선로는 단거리 선로에서 고려한 선로정수 R, L과 더불어 C까지 고려해야 합니다. 따라서 크게 두 가지 경우의 회로로 해석할 수 있습니다.
(1) T 회로
T회로는 선로 양단에 Z/2 씩, 선로 중앙에 Y로 집중한 회로입니다.
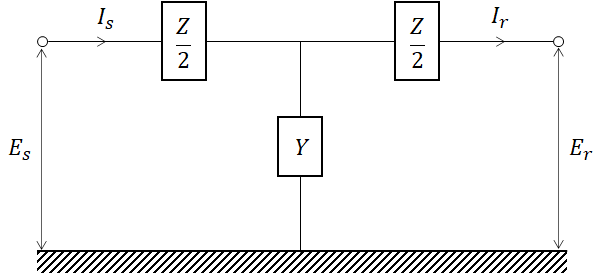
여기서 4단자 정수는 다음과 같습니다.
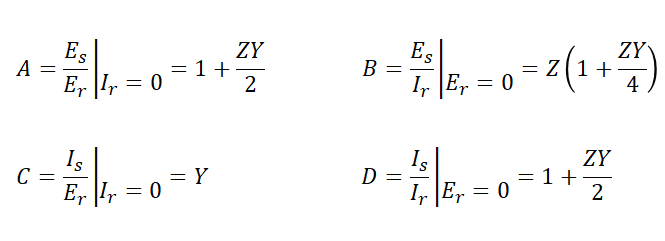
따라서 4단자 정수의 기본식에 대입하면 송전 전압과 송전 전류는 다음과 같이 구할 수 있습니다.
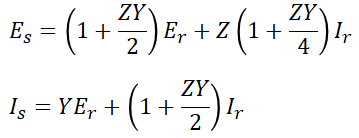
(2) π 회로
π 회로는 선로 양단에 Y/2 씩, 선로 중앙에 Z로 집중한 회로입니다.
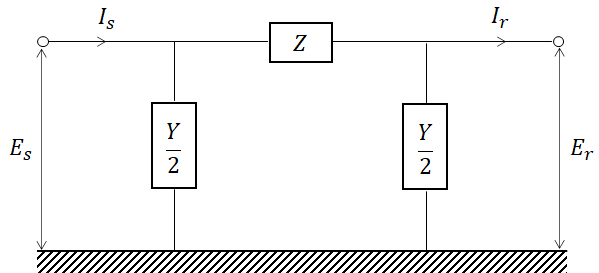
π회로에서의 4단자 정수는 다음과 같습니다.
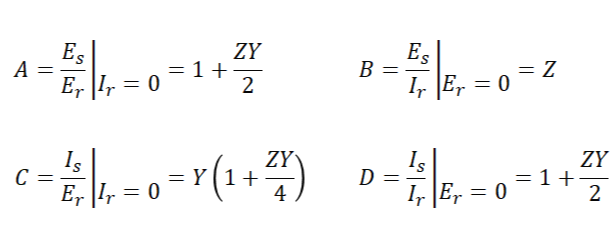
따라서 송전전압과 송전전류는 다음과 같이 구할 수 있습니다.

3) 선로의 병렬접속
두 가지의 4단자 망을 병렬접속하는 경우 다음과 같습니다.

위와 같은 경우 먼저 1회선 송전선로에 대한 송전단 전압과 전류를 계산하면 다음과 같습니다.
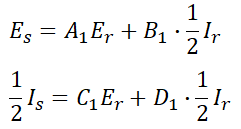
Is를 다시 쓰면,
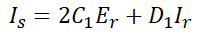
그리고 2회선 송전선로에 대해선 전체 4단자 정수를 A, B, C, D라고 했을 때, 다음과 같이 쓸 수 있습니다.

따라서 위의 식과 비교하면,

의 관계를 가지고 있습니다. 각각의 의미에 대해 다시 생각해보면, A와 D는 전압비와 전류비이므로 불변, 직렬 요소의 임피던스 값인 B는 병렬 접속이므로 1/2배 감소하고 병렬 요소의 어드미턴스 값인 C는 병렬접속이므로 2배 증가했다는 것을 알 수 있습니다.
4) 무부하 충전전류
4단자 정수가 A, B, C, D인 경우 4단자 정수로부터 송전단 전압과 전류가 다음과 같음을 알고 있습니다.
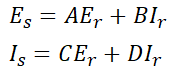
무부하 시는 Ir=0일 때 이므로 이를 대입하면

그리고,

로 구할 수 있습니다.
※ 참고 ※
위의 T와 π회로의 4단자 정수는 다음과 같은 방법으로 구할 수 있습니다.
1. T 회로

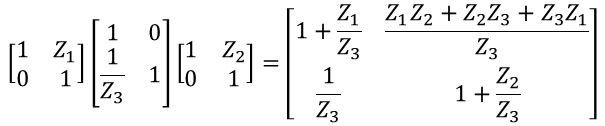
으로부터,
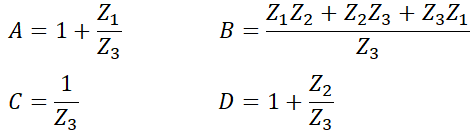
위의 T 회로에선 각각의 요소가 Z/2, Y이므로 이들을 대입하면 같은 결과를 얻을 수 있습니다.
2. π 회로
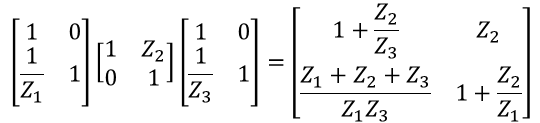
으로부터,

이며, 역시 위에서 살펴본 각각의 값들을 대입하면 같은 결과를 얻을 수 있습니다.
3. 장거리 송전선로
앞서 살펴 봤듯이 단거리 송전선로는 R과 L만의 직렬 회로로, 중거리 송전선로의 경우 R, L, C의 회로로 T회로와 π회로로 적용해 해석할 수 있었습니다.
장거리 송전선로는 여기에 g까지 추가해 R, L, C, g 모두 존재하는 것으로 다루어 분포 정수 회로를 이용해 풀어야 합니다. 장거리 송전선로는 특성임피던스와 전파정수를 이용해 해석하는데, 무부하 시험을 통해 어드미턴스 Y를 구하고, 단락시험을 통해 임피던스 Z를 구할 수 있습니다.
1) 특성 임피던스 Z0
특성 임피던스의 개념은 조금 복잡합니다. 송전선로의 어느 지점에서 입사파와 반사파의 차와 그 지점에서 전류와의 비를 의미합니다. 그러니 기사 수준에서, 그리고 장거리 송전선로의 해석에서는 단순히 전송선로가 가지는 고유의 임피던스로 어드미턴스와 임피던스의 비의 제곱근으로 기억하시면 됩니다.
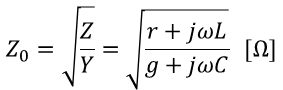
여기서 r은 선로 저항, g는 누설 컨덕턴스를 의미하는데, 장거리 송전선로에서는 L과 C의 영향이 커지기 때문에 특성 임피던스는 이를 무시하고 간단하게 다음과 같이 표현하기도 합니다.
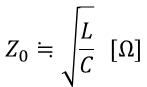
이렇게 r과 g가 0이 되는 선로를 무손실 회로라 하는 이상적인 경우를 말합니다.
2) 전파 정수 γ
전파 정수는 송전단으로부터 전압과 전류가 수전단으로 진행할 때 진폭과 위상 변화의 특성을 말합니다.
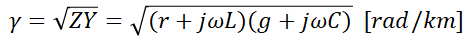
여기서 ω는 각속도, L은 작용 인덕턴스, C는 작용 정전용량을 말합니다. 역시 무손실 회로인 이상적인 경우라면 위의 식에서도 r과 g를 0으로 취급하여 계산하면 됩니다.
3) 인덕턴스와 정전용량
위에서 구한 특성 임피던스를 우리가 앞서 선로정수에서 구한 작용 인덕턴스와 정전용량을 대입해보면 다음과 같습니다.
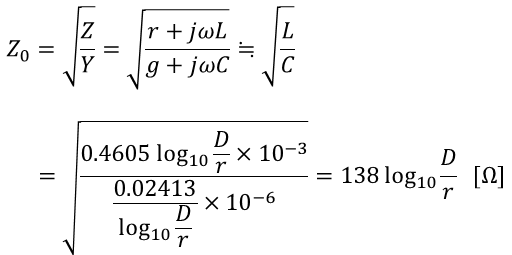
이를 이용해 인덕턴스와 정전용량은 다음과 같이 구할 수 있습니다.
(1) 인덕턴스
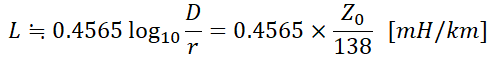
(2) 정전용량
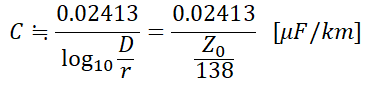
몇 가지 문제를 살펴보겠습니다.
ex.1) 그림과 같이 4단자 정수가 A1, B1, C1, D1인 송전선로의 양단에 Zs, Zr의 임피던스를 갖는 변압기가 연결된 경우 합성 4단자 정수 중 A의 값은?
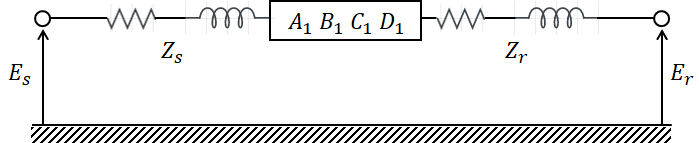
4단자 정수 양 옆으로 임피던스가 직렬로 연결되어 있으므로 다음과 같이 합성 4단자 정수를 구할 수 있습니다.

따라서 A는 A1+C1Zs가 된다는 것을 알 수 있습니다.
ex.2) 장거리 송전선에서 단위 길이당 임피던스 Z=r+jωL [Ω/km], 어드미턴스 Y=g+jωC [1/Ω/km]라 할 때 저항과 누설 컨덕턴스를 무시하는 경우의 특성 임피던스 값은?
먼저 특성 임피던스는 다음과 같이 구할 수 있습니다.

여기에 각각을 대입하고, 저항과 누설 컨덕턴스를 무하시하므로,

위와 같이 특성 임피던스를 구할 수 있습니다.
ex.3) 송전선로의 수전단을 단락한 경우 송전단에서 본 임피던스는 300 [Ω]이고, 수전단을 개방한 경우에는 1200 [Ω]일 때, 이 선로의 특성 임피던스는?
특성 임피던스는,

을 통해 구할 수 있습니다. 그리고 여기서 임피던스 Z는 단락시험을 통해, 어드미턴스 Y는 개방시험을 통해 얻은 값입니다. 따라서 문제의 조건에 따라 각각의 값을 대입하면,
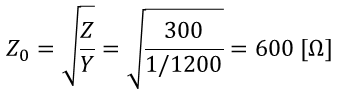
으로 구할 수 있습니다.
'전기 > 전력공학' 카테고리의 다른 글
| [전력공학] 6. 페란티 현상과 송전용량 및 전력계통의 연계 (0) | 2020.06.25 |
|---|---|
| [전력공학] 5. 전력원선도와 조상설비 (2) | 2020.06.17 |
| [전력공학] 4-1. 송전 특성_단거리 송전선로 (0) | 2020.06.08 |
| [전력공학] 3-2. 선로 정수 및 코로나 (1) | 2020.06.03 |
| [전력공학] 3-1. 선로 정수 및 코로나 (0) | 2020.06.02 |



