1. 선로정수
선로정수는 저항 R, 인덕턴스 L, 정전용량 C, 누설컨덕턴스 g의 4가지 정수를 말합니다. 선로정수는 전선의 종류, 굵기, 배치에 따라 정해지고 송전전압, 주파수, 전류, 역률, 기상 등에는 영향을 받지 않습니다. 따라서 리액턴스와 같이 주파수에 영향을 받는 요소들은 선로정수에 포함되지 않습니다. 그럼 각각에 대해서 살펴보도록 하겠습니다.
1) 저항 R
도체에서 전류의 흐름을 방해하는 정도를 나타내는 물리량으로 다음과 같이 표현할 수 있습니다.

여기서,

를 말합니다. 고유 저항은 도체에 따라 가지고 있는 고유의 저항 값으로 다음과 같습니다.

여기서, C는 도전율[%]을 뜻합니다. 전선에는 대표적으로 연동선, 경동선, 알루미늄선을 사용하는데 각각의 도전율이 다르므로 각기 다른 고유 저항을 가지고 있습니다.
| 도체 | 도전율[%] | 고유저항[Ω/mㆍ㎟] |
| 연동선 | 100 | 1/58 |
| 경동선 | 95 | 1/55 |
| 알루미늄선 | 61 | 1/35 |
2) 인덕턴스 L
전선에 전류가 흐르게 되면 자계가 발생하고 이 전류의 크기가 변하게 되면 전자유도에 의해 전압(역기전력)이 발생되는데, 이 때 이 전류 변화에 대해 발생되는 전압의 비율을 표시하는 양을 말합니다. 그리고 다음과 같이 크게 두 가지로 분류할 수 있습니다.
- 자기 인덕턴스 : 어떤 회로에서 전류가 변화하면 쇄교자속도 함께 변하게 됩니다. 그러면 이 변화를 막는 방향의 기전력이 회로에 발생하게 되는데 이를 자기 인덕턴스라고 합니다.
- 상호 인덕턴스 : 한 전기 회로에 다른 전기 회로가 근처에 있을 때 한쪽 전류르 변화시키면 이에 따라 자속이 변하게 됩니다. 이 변화가 다른 회로에도 영향을 미치게 되어 기전력이 유도되는 현상에 의한 인덕턴스를 말합니다.
보통 전력계통에서 이를 일체로 하여 1상에 대해 나타내고 있습니다.
선로정수에서의 인덕턴스는 어떤 도체를 사용하는지에 따라 조금 다른 방식으로 계산하게 됩니다.
(1) 단도체 인덕턴스

(2) 복도체 인덕턴스


여기서,

를 말합니다. 단도체와 복도체는 말 그대로 전선의 도체를 하나냐 둘 이상이냐를 말합니다. 도체를 하나 사용하는 선로의 경우 단도체 인덕턴스를 적용하고, 둘 이상인 경우엔 복도체 인덕턴스를 적용해 필요한 선로정수를 구하시면 됩니다.
① 등가 선간 거리
등가 선간 거리는 도체간 거리의 기하 평균거리를 말합니다. 인덕턴스의 계산시에는 대수항이 포함되어 있어 거리 및 높이의 계산에선 산술적 평균값을 이용할 수 없어 기하 평균을 취한 등가 선간 거리를 이용해 다음과 같이 계산해야 합니다.

간단한 예를 살펴보도록 하겠습니다.
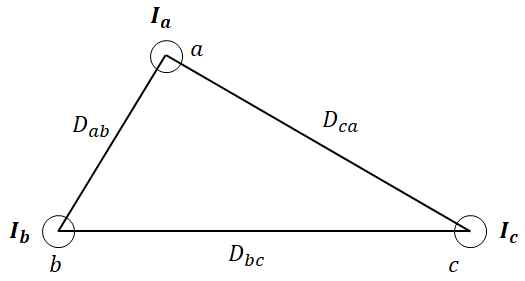
이런 식으로 도체가 분포 되어 있습니다. 3개의 도체가 있으므로 도체간 거리는 Dab, Dbc, Dca의 3가지가 있습니다. 그리고 이들이 각각의 거리를 말하고 있으니 등가 선간거리는 다음과 같이 계산할 수 있습니다.

등가 선간 거리는 같은 수의 도체를 사용하더라도 배열에 따라 값이 달라질 수 있습니다. 대표적인 예를 살펴보면 다음과 같습니다.
| 종류 | 그림 | 등가 선간 거리 |
| 수평 배열 |  |
 |
| 삼각 배열 |  |
 |
| 정사각 배열 |  |
 |
② 등가 반지름
복도체의 경우 반지름 역시 등가 반지름을 적용하여 인덕턴스를 계산해야 합니다. 등가 반지름은 다음의 식을 이용해 구할 수 있습니다.

여기서, n은 소도체 수, r은 소도체의 반지름, s는 소도체 간격을 말합니다. 복도체 인덕턴스를 구할 때 이 부분을 가장 유의해야 합니다. 복도체가 배열을 가진 경우엔 복도체 하나의 등가 반지름을 구하고, 복도체간 거리는 등가 선간 거리를 이용해서 계산하면 됩니다.
3) 정전 용량 C
(1) 작용 정전용량
작용 정전용량은 1선당 정전용량으로 대지 정전용량과 선간 정전용량의 합을 말합니다. 이 역시 단도체와 복도체를 구분해서 계산해 주어야 하고 전력 공급 방식에 따라서도 다르게 계산해야 합니다.
① 단도체 정전용량

② 복도체 정전용량

이때 역시 등가 반지름을 적용해야 합니다.
③ 부분 정전용량
- 단상 1회선
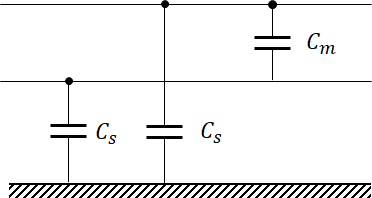
여기서 선간 정전용량을 둘로 나누게 되면 다음과 같이 나눌 수 있습니다.

그러면 이 둘을 각각의 상에서 지면과 연결하게 되면,
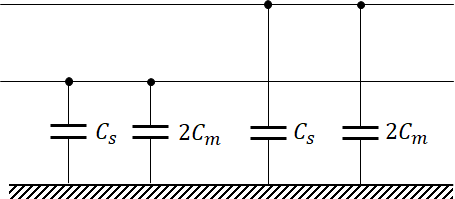
따라서 정리하면 다음과 같이 나타낼 수 있습니다.

즉, 단상 1회선인 경우의 부분 정전 용량은 다음과 같습니다.

여기서 각각은

을 의미합니다.
- 3상 1회선

이렇게 델타 결선으로 되어 있는 경우엔 대지 정전용량을 구할수가 없습니다. 따라서 등가의 Y결선으로 바꾸면 다음과 같습니다.
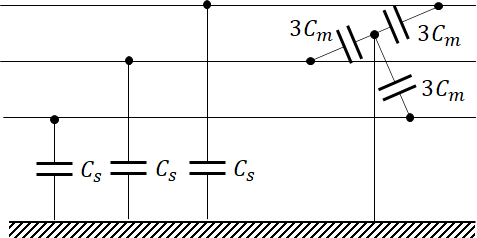
그럼 위와 같이 다시 정리하면,

다시 각각을 합치면 다음과 같습니다.

따라서 3상 1회선의 작용 정전용량은 다음과 같습니다.

④ 전선의 지표상 평균 높이
전선은 송전탑에 연결되어 쭉 이어져 있습니다. 그런데 지나가면서 보면 팽팽하게 연결되어 있는게 아니라 어느정도 느슨하게 연결되어 있는 것을 알 수 있습니다. 이는 전선의 온도 특성 때문인데, 여름에는 늘어지고 겨울에는 짧아지는 특성을 감안해 이로부터 전선을 보호하기 위해 어느정도 여유를 두는 것입니다.
이렇게 전선이 얼마나 늘어졌는지, 수직 방향으로 얼마나 내려가 있는지를 나타내는 것이 바로 이도입니다. 이도로 인해 측정하는 위치에 따라 전선과 지표면 사이의 높이가 다릅니다. 따라서 이 이도를 적용해 전선의 지표상 평균 높이를 구해야 하고, 다음과 같이 구할 수 있습니다.

h'은 지지점의 높이 [m], d는 이도(dip) [m]을 의미합니다.
(2) 충전 용량
① 전선의 충전 전류

여기서 C는 전선 1선당 정전 용량 [F], V 는 선간 전압 [V]을 의미합니다. 여기서 알 수 있듯이 선로의 충전전류를 계산할 때 전압은 변압기의 결선과 관계 없이 상전압을 적용해야 합니다. 그림으로 살펴보면,

여기서 대지를 한 점으로 연결하면 다음과 같이 그릴 수 있습니다.

이렇게 항상 상전압을 적용해야 한다는 것을 알 수 있습니다.
② 전선로의 충전 용량

(3) 정전용량의 적용
정전용량은 어떤 전류를 계산하는지에 따라 필요한 정전용량을 적용해야 합니다.
- 지락전류 계산 : 대지 정전용량 적용

- 충전전류 계산 : 작용 정전용량 적용

4) 누설 컨덕턴스 g
애자에 의해 전선 상호간과 전선과 대지 사이를 절연하지만 완전한 절연은 아니기 때문에 약간의 누설전류가 흐르게 됩니다. 이로 인해 유전체 손실, 히스테리시스 손이 발생하게 되어 이 손실을 표현하기 위해 누설저항을 등가적으로 나타낼 수 있습니다. 컨덕턴스는 저항의 역수로 이 등가적으로 나타낸 누설저항의 역수가 바로 누설 컨덕턴스 입니다.
2. 연가
송전선로의 길이를 3의 정수배 구간으로 등분해 지상의 전선을 적당한 구간마다 바꾸어 아래와 같이 전체적으로 평형시키는 것을 연가라고 합니다.

이 연가가 필요한 이유는 일반적인 3상 3선식 선로에서 정삼각형 배치가 아니기 때문입니다. 또한 지표상의 높이도 서로 같지 않기 때문에 각 전선의 인덕턴스나 정전용량이 다르게 됩니다. 이렇게 되면 송전단에서 대칭전압을 인가하더라도 수전단에서는 비대칭으로 받게 될 것입니다. 따라서 이를 평형시키기 위해 위 처럼 연가하여 전선간 평형을 유지할 수 있도록 합니다.
이런 연가로 얻을 수 있는 효과로는 직렬공진의 방지, 유도장해 감소, 선로정수의 평형이 있습니다.
'전기 > 전력공학' 카테고리의 다른 글
| [전력공학] 4-2. 송전 특성_중거리 송전선로와 장거리 송전선로 (0) | 2020.06.08 |
|---|---|
| [전력공학] 4-1. 송전 특성_단거리 송전선로 (0) | 2020.06.08 |
| [전력공학] 3-2. 선로 정수 및 코로나 (1) | 2020.06.03 |
| [전력공학] 2. 역률의 특성과 전기요금 (0) | 2020.02.06 |
| [전력공학] 1. 역률 (0) | 2020.02.04 |



