3. 발전기 고장 계산
발전기 고장에는 대표적으로 1선 지락, 2선 지락, 선간 단락, 3상 단락 고장이 있습니다. 각각의 경우 이전 포스팅에서 살펴본 대칭 좌표법에 의해 어떻게 계산하는지 살펴보도록 하겠습니다.
1) 1선 지락 고장
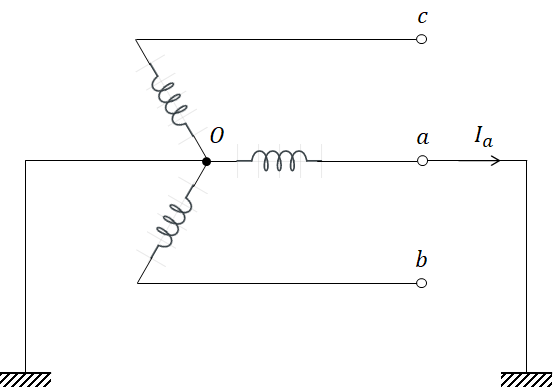
그림과 같이 a상에 지락이 발생한 경우 입니다. 따라서 다음과 같은 사실을 먼저 알 수 있습니다.
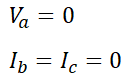
여기서 우선 b상과 c상의 전류를 대칭좌표법으로 보면,
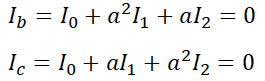
이므로 Ib-Ic를 하면,
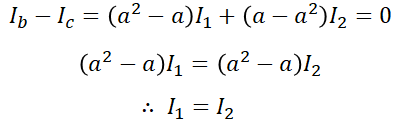
이라는 것을 알 수 있습니다. 여기서 다시 이 값을 Ib 식에 대입하면,
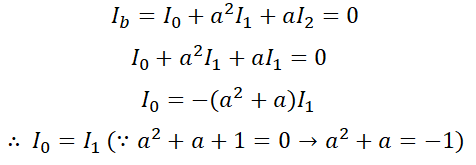
따라서 I0=I1=I2라는 사실을 알 수 있습니다. 그럼 Ia에 대해 정리하면,
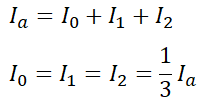
라는 것도 알 수 있습니다.
다음으로 발전기 기본식으로부터 우리는 다음과 같은 식을 찾을 수 있습니다.
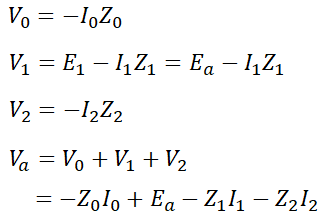
그런데 Va=0이고, I0=I1=I2이므로 I0로 정리하면,
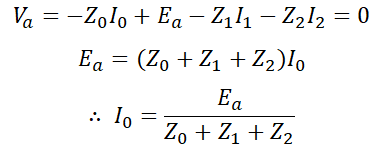
따라서 지락전류를 구하면,
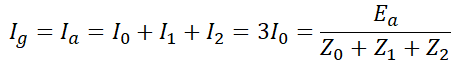
으로 구할 수 있습니다.
대칭분 전압의 경우 이렇게 구한 전류를 대입해 구할 수 있습니다.
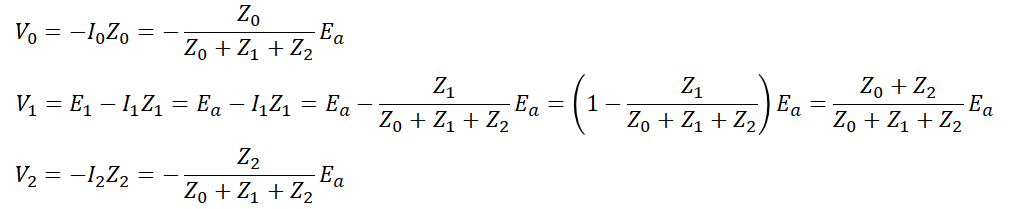
이를 이용해 b상과 c상의 전압까지 구하면,
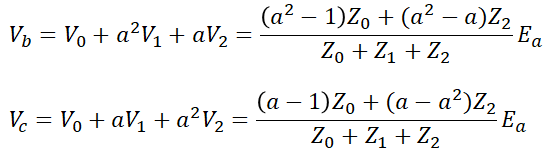
위와 같이 구할 수 있습니다.
2) 2선 지락 고장
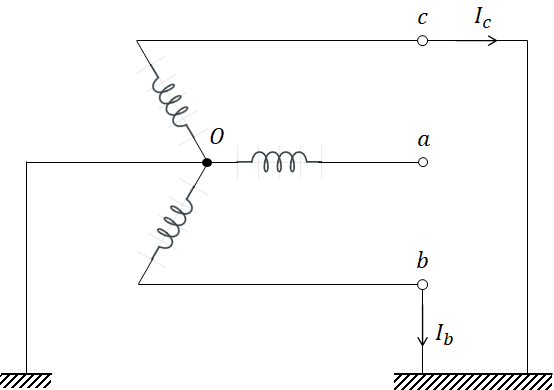
b상과 c상에 지락이 발생한 경우로 먼저 다음과 같은 사실을 알 수 있습니다.
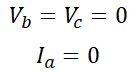
Vb와 Vc가 0이므로 위의 1선 지락의 경우에서 전류와 같이 단자 전압의 대칭분은,
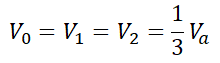
라는 것을 알 수 있습니다. 이를 발전기 기본식에 적용하면,
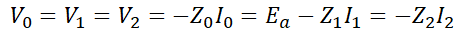
또,
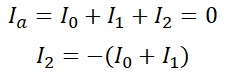
이므로, 위 식에 대입하면,
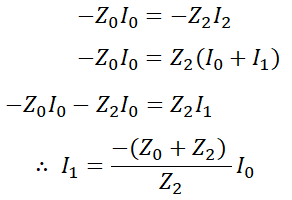
라는 것을 알 수 있습니다. 이를 다시 위의 발전기 식의 다른 관계에 대입하게 되면,
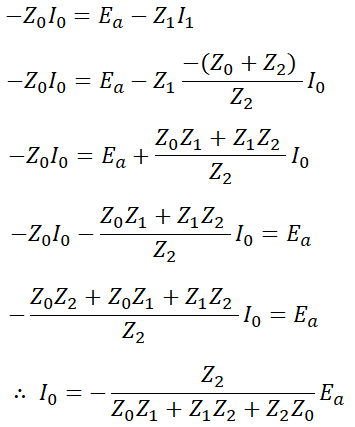
위와 같이 I0를 구할 수 있습니다. 그럼 I1는,
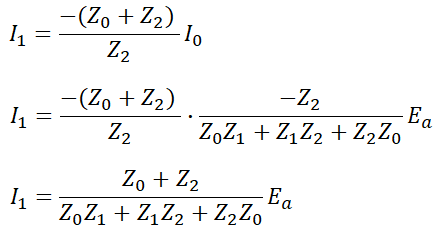
이어서 I2는,
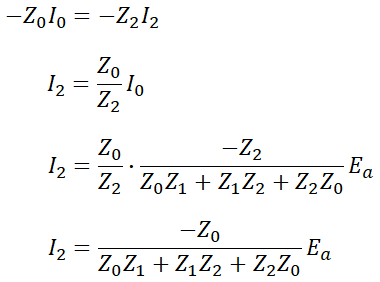
다음으로 대칭분 전압의 경우
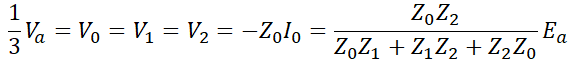
이고, 지락 전류 Ib와 Ic는 각각을 대입해 정리하면,
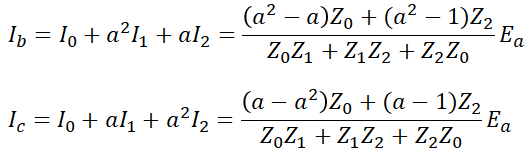
라는 것을 알 수 있습니다.
3) 선간 단락 고장
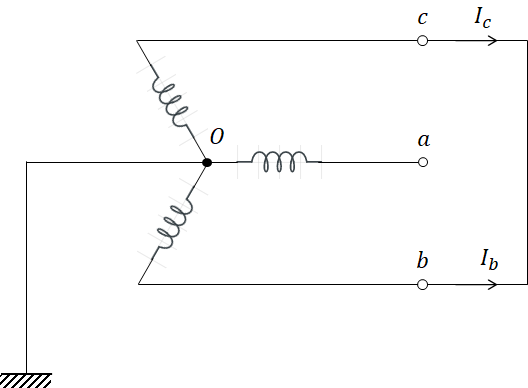
b상과 c상이 단락된 경우로 먼저 다음의 사실을 알 수 있습니다.
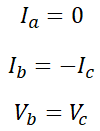
이를 활용해 먼저 대칭분 전압을 구하면,
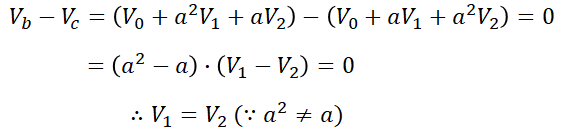
대칭분 전류 역시 구할 수 있습니다.
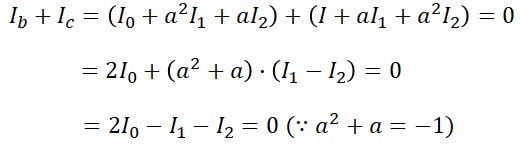
여기서, Ia=0 이므로,
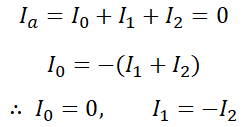
그럼 이들을 발전기 기본식에 대입하면,
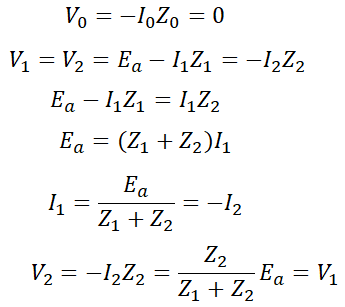
와 같이 구할 수 있습니다.
이로부터 각 상의 전압과 전류를 구하면,
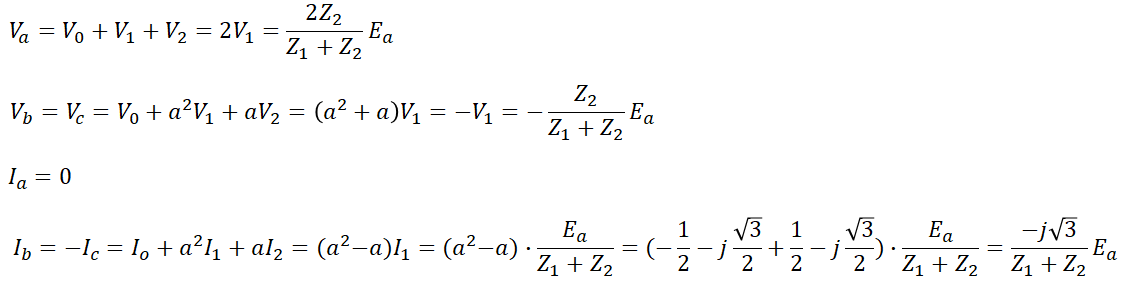
와 같이 구할 수 있습니다.
4) 3상 단락 고장
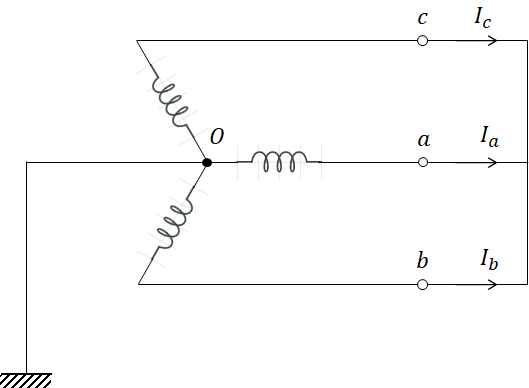
3상이 모두 단락된 경우입니다. 따라서 다음과 같은 식이 성립하게 됩니다.
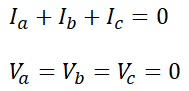
먼저 대칭분 전압을 계산하면,
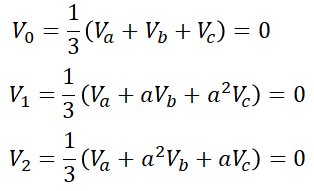
각 상의 전압이 0이기 때문에 당연히 대칭분 전압도 0이 되게 됩니다. 이를 발전기 기본식에 대입하면,
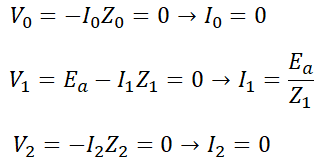
으로 대칭분 전류도 구할 수 있습니다. 이를 이용해 각 상의 전류를 구하면,
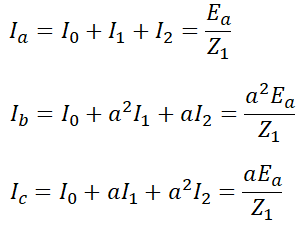
로 구할 수 있습니다.
'전기 > 전력공학' 카테고리의 다른 글
| [전력공학] 9. 중성점 접지 방식 (0) | 2020.07.14 |
|---|---|
| [전력공학] 8. 유도 장해와 안정도 (0) | 2020.06.29 |
| [전력공학] 7-2. 고장 계산_ 대칭 좌표법 (1) | 2020.06.25 |
| [전력공학] 7-1. 고장 계산_ 단락 고장 (0) | 2020.06.25 |
| [전력공학] 6. 페란티 현상과 송전용량 및 전력계통의 연계 (0) | 2020.06.25 |



