2. 반지름 a, b(b>a) [m]의 동심 구도체 사이에 유전율 ε[F/m]의 유전체가 채워졌을 때의 정전용량은?
동심구의 내구와 외구 사이의 전위차는,

따라서 정전용량은,

3. 맥스웰 방정식?
| 맥스웰 방정식 | 미분형 | 적분형 |
| 가우스 법칙 |  |
 |
| 가우스 법칙 | 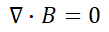 |
 |
| 암페어의 주회 법칙 |  |
 |
| 패러데이 법칙 |  |
 |
4. 특성임피던스가 각각 η1, η2인 두 매질의 경계면에 전자파가 수직으로 입사할 때 전계가 무반사로 되기 위한 가장 알맞은 조건은?
전자파의 반사계수 R은 다음과 같습니다.

무반사가 되기 위한 조건은 R=0이므로,

즉, 두 매질의 특성임피던스가 같을 때 무반사가 된다는 것을 알 수 있습니다.
6. 반지름 a[m]의 원형 단면을 가진 도선에 전도전류 ic=Ic sin 2πft[A]가 흐를 때 변위 전위밀도의 최대값 Jd는?(도전율은 σ[S/m], 비유전율은 εr)
전도전류밀도는,
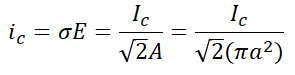
이므로 여기서,

변위전류밀도는,

이므로 변위전류밀도의 최대값 Jd는,

가 됩니다.
7. 무한 평면도체로부터 거리 a[m]인 곳에 점전하 Q[C]가 있을 때 도체 표면에 유도되는 최대전하밀도는?
무한 평면도체상의 기준 원점으로부터 거리 a[m]인 곳에 있는 점전하 Q[C]에 의해 유도되는 전하밀도는

입니다. 따라서 y=0에서 최대, y=∞에서 최소이므로,


가 됩니다.
8. 자속밀도가 0.3[Wb/m^2]인 평등자계 내에 5[A]의 전류가 흐르고 있는 길이 2[m]인 직선도체를 자계의 방향에 대하여 60º의 각도로 놓았을 때 이 도체가 받는 힘은?
평등 자계 내에서 도체가 받는 힘은 다음과 같습니다.
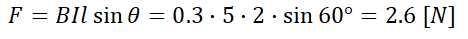
9. 2[C]의 점전하가 전계 E=2ax+ay-4az [V/m], 자계 B=-2ax+2ay-az[Wb/m^2]내에서 속도 v=4ax-ay-2az[m/s]로 운동하고 있을 때 점전하에 작용하는 힘 F?

10. Q[C]의 전하를 가진 반지름 a[m]의 도체구를 유전율 ε[F/m]의 기름 탱크로부터 공기중으로 빼내는데 요하는 에너지는?
공기중의 구의 용량을 C, 기름 중의 구의 용량을 C'라 하면,
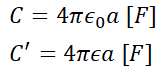
따라서 필요한 에너지 W는 다음과 같습니다.

11. 다음 설명 중 옳은 것은?
- 자계 내의 자속밀도는 벡터포텐셜을 폐로선적분하여 구할 수 있다.
벡터포텐셜의 폐로선적분은 자속입니다.

- 벡터포텐셜은 거리에 반비례하며 전류의 방향과 같다.
벡터포텐셜은 다음과 같습니다.

따라서 벡터포텐셜은 거리에 반비례하고 전류의 방향과 같습니다.
- 자속은 벡터포텐셜의 curl을 취하면 구할 수 있다.
벡터포텐셜의 curl을 취하면 자속밀도를 구할 수 있습니다.

- 스칼라포텐셜은 정전계와 정자계에서 모두 정의되나 벡터포텐셜은 정전계에서만 정의된다.
스칼라포텐셜은 정전계와 정자계에서 모두 정의되지만 벡터포텐셜은 정자계에서만 정의됩니다.
12. 비투자율 350인 환상철심 중의 평균 자계의 세기가 280[AT/m]일 때 자화의 세기는?
자화율은,

이므로, 자화의 세기는,

13. 한 변의 저항이 R0인 그림과 같은 무한히 긴 회로에서 AB간의 합성저항은?

무한히 긴 회로이므로 반복되는 부분을 찾아야 합니다. 먼저 CD에서 우측으로 본 합성저항을 R이라 하면,

위 그림과 같습니다. 그럼 AB에서의 합성저항을 R_AB라 하면,

그리고 무한한 선로이기 때문에 이 R_AB는 결국 R과 같다고 볼 수 있습니다. 따라서,
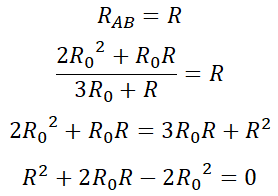
따라서 구하고자하는 R은,

14. 평면 전자파가 유전율 ε, 투자율 μ인 유전체 내를 전파한다. 전계의 세기가 E=Em sinω(t-x/v) [V/m]라면 자계의 세기는?
평면 전자파의 고유임피던스는 다음과 같습니다.
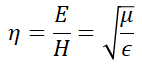
따라서 자계의 세기 H를 구하면,

17. 전계 E[V/m]가 두 유전체의 경계면에 평행으로 작용하는 경우 경계면의 단위 면적당 작용하는 힘은?
전계가 경계면에 평행인 경우에 작용하는 힘은,

이며 유전율이 큰 쪽에서 유전율이 작으 ㄴ쪽으로 끌려 들어가는 맥스웰 응력이 작용합니다.
18. 지름 2[mm], 길이 25[m]인 동선의 내부 인덕턴스는?
동축 케이블의 내부인덕턴스는 다음과 같습니다.

그리고 동선의 경우 μ≒μ0 이므로,

19. 그림과 같은 자기회로에서 A부분에만 코일을 감아서 전류를 인가할 때의 자기저항과 B부분에만 코일을 감아서 전류를 인가할 때의 자기저항을 각각 구하면?(R1=3[AT/Wb], R2=1[AT/Wb], R3=2[AT/Wb])

- 먼저 A부분에만 코일을 감아서 전류를 인가할 때의 회로는 다음과 같습니다.

그럼 R2와 R3가 병렬이고 둘의 합성저항이 R1과 직렬로 연결되어 있으므로 전체 합성저항을 R_A라하면 R_A는,

- B부분에만 코일을 감아서 전류를 인가할 때의 회로는,

그럼 R1과 R3가 병렬, 이 둘의 합성저항이 R2와 직렬이므로 전체 합성저항을 R_B라 하면,

로 구할 수 있습니다.
'전기 > 전기기사 문제풀이' 카테고리의 다른 글
| [전기기사] 2015년 3회. 전기기기_41~60 (0) | 2020.09.27 |
|---|---|
| [전기기사] 2015년 3회. 전력공학_21~40 (0) | 2020.09.27 |
| [전기기사] 2015년 2회. 회로이론 및 제어공학_61~80 (0) | 2020.09.25 |
| [전기기사] 2015년 2회. 전기기기_41~60 (0) | 2020.09.24 |
| [전기기사] 2015년 2회. 전력공학_21~40 (0) | 2020.09.24 |



