앞서 정상편차에 대해 알아보며 이 정상편차는 다음과 같은 식에 의해 구할 수 있다는 것을 보았습니다. 그리고 이 식으로부터 편차의 존재를 결정짓는 것은 G(s)라는 것도 알 수 있습니다.

따라서 바로 이 전달함수 G(s)로부터 제어계를 분류하고 있습니다.
1. 형에 의한 제어계의 분류
전달함수 G(s)는 입력과 출력에 의해 나타나고, 분모와 분자가 s에대한 고차항으로 나타납니다. 또한, 다양한 극점과 영점이 존재하고 있다면 이 전달함수 G(s)는 다음과 같이 표현할 수 있습니다.

이 식을 다시 풀어쓰게 되면,

분모, 분자항의 상수항을 1로 만들기 위해 새로운 상수 k를 도입하여 정리하였습니다. 그러나 위 정상편차의 식으로부터 우리가 궁금했던 것은 정상편차에서 분모의 형태였습니다.
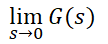
따라서 이 극한값이 어떤 형태를 띄는지가 바로 제어계를 분류하는 기준이 되는 것입니다. 결국,
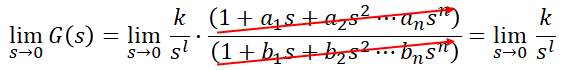
이 되므로, 여기서 l의 값에 의해 제어계의 형이 결정된다는 것을 알 수 있습니다. 그리고, 여기서 l의 값에 따라 제어계를 다음과 같이 분류를 하게 됩니다.
1) l=0 : 0형 제어계
2) l=1 : 1형 제어계
3) l=2 : 2형 제어계
이와 같은식으로 l=n 이라면 n형 제어계가 되는 것입니다. 다음의 입력에 따른 정상편차를 보게되면 이해하기 쉬울 것입니다.
2. 기준입력시험에 대한 정상편차
기준입력은 지금까지 살펴보았던 위치, 속도, 가속도입력을 말합니다. 그럼 각각의 경우에서 정상편차를 한 번 살펴보도록 하겠습니다.
1) 정상 위치 편차

이러한 입력을 우리가 알고있는 정상편차 식에 대입해보도록 하겠습니다.

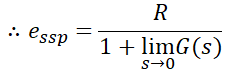
다음에 나올 정상속도편차와 가속도편차로부터 구분을 짓기 위해 첨자p를 사용했습니다. 여기서 형에 따른 제어계의 G(s)값들을 대입해보도록 하겠습니다.
(1) 0형 제어계

그럼 정상위치편차는
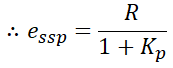
여기서 Kp를 정상위치편차 상수라고 말합니다.
(2) 1형 제어계
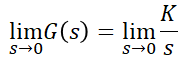
l=1일 때이므로 위와 같은 형태로 나올 것입니다. 이를 대입하면,

분모항이 무한대로 발산하기 때문에 결국 1형 제어계에서 정상위치편차는 0이 된다는 것을 알 수 있습니다. 따라서 1형 이상의 제어계는 계속해서 G(s)의 극한값이 무한대가 나오므로 모두 정상편차는 0이 될 것입니다.
2) 정상 속도 편차
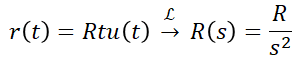
이 입력을 정상편차 식에 대입하게 되면,
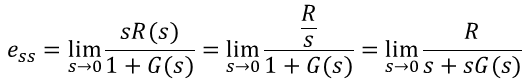

가 된다는 것을 알 수 있습니다. 역시 형에 따라서 살펴보도록 하겠습니다.
(1) 0형 제어계

이므로, 위 식에 대입하면,
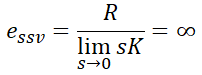
로 발산한다는 것을 알 수 있습니다.
(2) 1형 제어계

이 값을 위에 대입하게 되면,
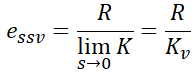
로 나타나게 됩니다. 역시 Kv를 정상속도편차상수라고 합니다.
(3) 2형 제어계
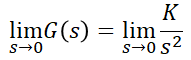
이므로 정상편차식에 대입하면,
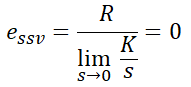
즉, 정상속도편차는 2형 제어계 이상에서 편차는 0이라는 것을 알 수 있습니다.
3) 정상가속도편차

이제 입력을 보면 어떤 형태로 나오게 될지 감이 오셨을 겁니다. 정상편차를 살펴보면


와 같은 형태로 나오므로 2형제어계에서 정상편차가 존재할 것이라는 것을 예상할 수 있습니다.
(1) 0형 제어계

이므로 정상가속도편차는,

로 나타납니다.
(2) 1형 제어계

이므로 정상가속도편차는,

가 됩니다.
(3) 2형 제어계
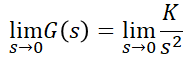
이므로 정상가속도편차는,
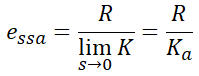
가 되고, 역시 Ka를 정상가속도편차상수라고 말합니다.
(4) 3형 제어계
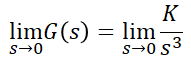
이므로 정상가속도편차는,

가 되므로, 3형 이상의 제어계에서 정상가속도편차는 0이 된다는 사실을 알 수 있습니다.
몇 가지 예제를 살펴보도록 하겠습니다.
ex.1) 개루프 전달함수가 다음과 같을 때, 단위 계단 입력에 대한 정상편차를 구하시오.

단위계단입력이므로 R=1이고, 정상위치편차를 구하면 됩니다. 따라서

으로부터 분모의 limG(s)에 주어진 G(s)를 대입하면


정상편차를 구해야하므로 꼭 essp에 구한 Kp를 대입해서 구해야 합니다.
ex.2) 개루프 전달함수가 다음과 같을 때, 단위 속도 입력에 대한 정상편차를 구하시오.
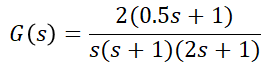
위에서 정상속도편차는 다음과 같았습니다.
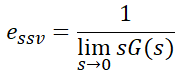
역시 단위속도입력이므로 R=1이고, 따라서 주어진 G(s)를 대입하면,

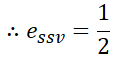
로 구할 수 있습니다.
ex.3) R(s)와 G(s)가 다음과 같은 단위 Feed-back 제어계에서의 정상편차를 구하시오.

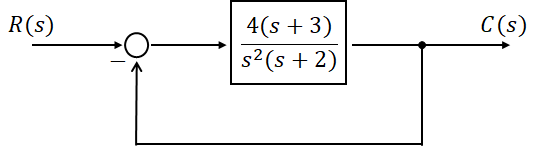
먼저 정상편차를 구해야 하므로

에 주어진 값들을 대입하여 구하면 됩니다. 하지만, 위 블록선도에서 알 수 있듯이 G(s)가 2형 제어계이므로 정상가속도편차만 존재할 것입니다. 따라서 주어진 입력에서 우리가 고려해야 할 것은
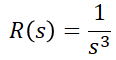
항만 고려하면 됩니다. 따라서,

로 구할 수 있습니다.
'전기 > 제어공학' 카테고리의 다른 글
| [제어공학] 10. 보드선도 (0) | 2020.01.25 |
|---|---|
| [제어공학] 9. 주파수 응답과 벡터 궤적 (2) | 2020.01.22 |
| [제어공학] 7. 과도응답의 시간특성 및 정상편차 (0) | 2020.01.22 |
| [제어공학] 6. 특성방정식의 근의 위치별 응답특성 (0) | 2020.01.22 |
| [제어공학] 5. 1차, 2차 지연 제어계의 과도 응답 (1) | 2020.01.20 |



